World War I in Real Time: First Edition Problems

I’m teaching out of my World War I game theory textbook for the first time this semester, and as I worked through some early-morning class prep this morning, I noticed a tiny little error in Chapter 2. But worry not: all the equilibria still exist, and for the same reasons. It’s a typo, but one worth clarifying.

What’s the issue?

Section 2.2, “Commitment Problems and War,” motivates a game in which state A has to decide whether to launch a preventive war in light of the possibility that B, who’s rising in strength, might renege on the status quo in the future. And in describing A’s payoffs, I say that its best outcome of a peacefully honored status quo gives it 4, its worst outcome of passing on war only to see the status quo renegotiated is 1, and the middling outcome of launching a preventive war today is 2. That’s true whatever B’s strategy happens to be, because that strategy is preempted by A’s use of war.

That … makes sense.

But for some reason, in Figure 2.5 (rendered below), A gets 2 for the outcome of the (attack; honor) strategy profile and 3 for the (attack; renege) strategy profile. That’s…unnecessary. A should really get 2 for both, unless we want to say that attacking a B that would’ve honored the agreement is regrettable, but that’s not necessary for the story. It’s also not in my initial description of the payoffs.

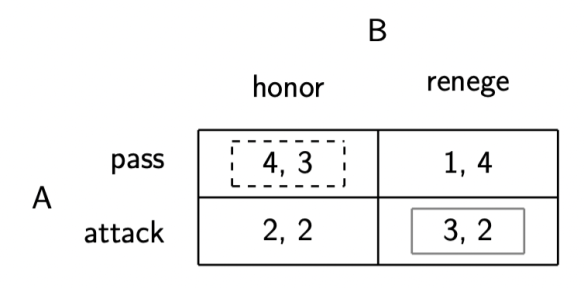
Now, as you’ll see, the Nash Equilibrium of the game (marked by the solid gray lines) is the same whether that offending 3 is in there or is replaced by the intended 2:

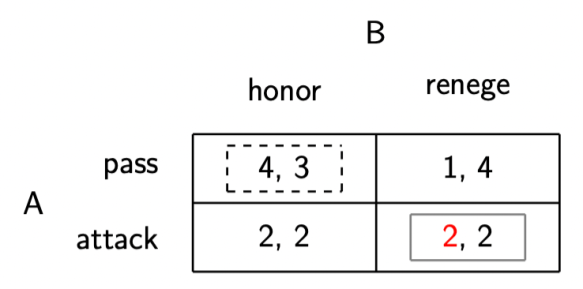
But I don’t want to let errors like this pass without some kind of note to adopters and students and whoever else has posts on this blog inflicted on them. So, apologies, dear reader(s). Let’s hope there aren’t too many more posts like this one forthcoming.

My own buffoonery aside, there’s a useful point here: forcing ourselves to “do the math” means we can more easily find, correct, and assess the consequences of mistakes in our premises and/or our reasoning. That’s always and everywhere a good thing for the social scientist.

On the relationship between information problems and commitment problems

Most political scientists that study conflict are familiar with a pair of bargaining frictions that, on their own, can cause negotiations to break down in war: (a) information problems and (b) commitment problems. Fearon’s famous IO piece distinguishes them from one another as solutions to the inefficiency puzzle of war—i.e., why fight when peaceful negotiation can produce the same outcome without all the waste? But in scholarly practice there seems to be widespread confusion about the relationship between these two mechanisms, both in terms of where one ends and the other begins and whether/how they interact. In this post, I’m going to (try to) clear it up.

tl:dr at the bottom.

The curious(ly limited) naval war (WWI in Real Time, Lecture 17)

The pre-war naval race and general British mastery of the seas notwithstanding, one of the more puzzling aspects of the First World War is the absence of large-scale naval campaigns. Neither the British nor the Germans committed to a full-scale naval war for mastery of the North Sea—which could’ve been pretty valuable for both of them—and Germany chose not to use its U-boats to their greatest (i.e., unrestricted) potential in 1914. While their armies clashed on a nearly apocalyptic scale on the Continent, their navies were largely sidelined. But why? We spent time in class today on this very puzzle, and, as luck would have it, I got to work out some ideas from a model that I’ll be workshopping tomorrow with the IR group here at Texas.

The answer, I think, lies in recognizing that fighting is not only costly upfront but also in terms of military capabilities or assets that, once lost, aren’t easily replaced; in other words, for both the British and German navies, using it also meant losing it. Stevenson captures this logic well:

The weaker side had little motive to risk annihilation, nor the stronger to risk nullifying its lead (p. 199)

Had the Germans and British gone all out in fighting for control of the North Sea, the costs in terms of forces-in-being might’ve been substantial. The Germans, of course, might’ve lost so much of their weaker force that, even in a short-term victory, they’d be unable to deter future moves towards their coast. Likewise, the British were stretched across the globe, protecting shipping and controlling the worldwide network of coaling stations that allowed them to exert pressure on neutrals—committing forces to replace any lost in a major naval war or to beef up coastal defense at home might’ve compromised this position. So, given dubious gains—the promise of blockade without a naval war, the difficultly of an amphibious assault on northern Germany, the British ability to rebuild lost ships in the medium term—it looks like both sides found plenty of reasons to keep their naval forces intact and keep this one small aspect of the war from approaching totality.

We drew the following game to capture the situation,

which actually shows that the no-fighting equilibrium isn’t unique. Even if each side wanted to husband its naval capabilities, it would’ve fought had it believed that the other would’ve. That seems trivial, but it also explains some interesting features of the war, such as the occasional battle—Heligoland Bight and Dogger Bank in 1914—but the lack of sustained campaigns and each side’s willingness to refuse to press the attack on a grad scale, even if the other side was on the run. Which equilibrium prevails—fighting or no-fighting—depends on each side’s beliefs about the other’s strategy, and these can be fragile things in the fog of war…which I guess in the North Sea is both figurative and literal. When beliefs about the other side’s likely strategy were stable, we saw a pretty persistent no-fighting equilibrium, but all it would take for a switch to the occasional battle was a change in beliefs about likely strategies, not a change in the actual strategic situation.

Of course, this leaves aside the question of why Germany kept the U-boats restrained during 1914, but we’ll get to that soon enough…

strategy, equilibrium, and tragedy (WWI in Real Time, Lecture 2)

After setting the table in Tuesday’s lecture, today was about practicing one of the key tools we’ll use in trying to make sense of the First World War: game theory (especially the associated concepts of strategy and equilibrium). Each week, we’ll address a puzzling outcome—for example, the outbreak or expansion of the war—by thinking about how political actors doing their best to pursue their goals (however defined) might find themselves making the choices that they do. In politics generally, but in this course in particular, one of they key parts of any story has to be strategic interaction: that is, how actors make choices in anticipation of what others will do, and how those choices add up to something often quite surprising (or, often, something quite tragic). Game theory is designed to do just that, and today we illustrate how we’ll use the tool with a simple pre-war puzzle: the Anglo-German Naval Race.

The Puzzle(s) of the Great War (Teaching WWI in Real Time, Lecture 1)

So the day has finally arrived: I’ve just finished the first lecture of the semester in World War I in Real Time (syllabus here). The buildup’s been long, the conversations with friends and loved ones likely one-sided and (for them) tiresome, but now it’s all going to be targeted at my students.* (Sorry, folks.)

Today’s lecture is really about setting the table; we won’t be digging into anything just yet. The first task will be to situate us on 2 September 1914, when

1. The German armies reach the River Marne after crashing through neutral Belgium, though the right wing has managed to turn ever so slightly too soon….
2. The French government, sensing the vulnerability of their capital, flees Paris for the relative safety (not the wine) of Bordeaux, while the Army (with a little help from its British friends) effects a grand retreat of its own.
3. Austro-Hungarian armies fall back in the face of a Russian onslaught in Poland and Galcia, allowing the latter to capture (what is in 1914 called) Lemberg (but will go by Lvov and Liviv at different times in the coming decades).

We’re about a month into the war, with France, Russia, and the UK squaring off against Germany and Austria-Hungary in a war that The Economist on 8 August has already described as “perhaps the greatest tragedy of human history.” Many thousands already lay dead, and many millions will go on to die in the coming years.

The questions we’ll then pose in the course are how we got here—where “here” means a world with all the Great Powers (save one) at war—and why the war looks the way it does, both at the front and behind the lines.  As I’ve noted before, we’ll use the sparest tools of game theory to think about how goals, means, and incentives (where the latter two have something to do with others’ goals, means, and incentives) add up to produce outcomes that are non-obvious, sometimes surprising, and, surely in the context of 1914, very often tragic.

Next up, a class of tool-building, where we talk about our core concepts of strategy, equilibrium, and tragedy.

* Really. I couldn’t help myself, even at APSA: “Hey, you study repression, right? How interesting is it that the German army’s treatment of civilians was so bad in Belgium, but it virtually stopped once they got to France? Right? Right?” And who could forget, “You study roads and counterinsurgency, eh? Did you know that the Russian rail network in 1914 was intentionally bad in places to stem a feared German invasion? Can you guess how that played out when the Russians needed to attack to the west? Can you?” To the targets of these outbursts, I say: you’re welcome.

Leaping into the dark, Bethmann-style (Teaching WWI in Real Time)

As the realization of what I committed to with my World War I In Real Time fall course starts to dawn on me—centennials will do that to you, I suppose—I figured the anniversary of the Sarajevo assassinations would be an opportune time to share what I’ve been doing in preparation for the course, as well as what I’ve learned, not so much about the War but about prepping a new, and highly specific, course.

1. This is going to be a lot of work. (Shocking, right?) I suppose this dawning realization is also apropos, at least with respect to the war itself; committing to this course was a leap in the dark, so to speak, one taken with no small amount of blind enthusiasm, but I don’t think I’ll be quite so regretful as Bethmann Hollweg was after his. <fingers crossed>
2. I’m almost relieved that, on the first day of class (28 August), we’ll be past the July Crisis. Sure, the immediate sparks of the war can be found there, and I won’t be able to make proper use of “Take me Out” by Franz Ferdinand (h/t YL), but I have a sense that I’d be as impatient as Germany waiting for Austria to get off the blocks—and spending too much lecture time on pre-war crises than I really want.
3. It’s too bad that the Battle of the Frontiers will have just ended, but the day of the 28th is fraught with contingency, choice, and uncertainty—-the perfect stuff, I think, of a first lecture. German armies have crashed through neutral Belgium, hoping to achieve a modern-day Cannae on a massive scale, only to be lured into turning south too soon, foregoing the envelopment of Paris while chasing the possibility of eliminating the French now in the field. General Joffre, on the other hand, has come to the conclusion that attrition might be the only way to win the war, and his famous General Instruction No. 2 will have just gone out, precipitating a massive retreat and repositioning Allied forces so as to set up what would become known as the Battle of the Marne—the moment(s) when Moltke’s version of the Schlieffen plan would be dashed for good, and when the Western Front would begin to settle into what we all know it, now, to look like. 28 August also sees Joffre meeting with Sir John French, trying to keep the British Expeditionary Force in the line, setting the stage for years of (what I, at least, think are) fascinating intra-coalitional politics. With plans wrecked, opponents adjusting, and the strategic picture in remarkable flux, what will the generals, the soldiers, the statesmen, and the home fronts do in response? Forgive me if that’s a goosebump moment for me; I can’t wait to give this lecture.
4. Lengthy geek-out aside, I’m assigning Max Hastings’ Catastrophe,  which pretty much covers the war from August to the end of the semester—and which I hope my undergrads find to be sufficiently readable. (Well, those that read enough to judge readability, I should say.) As for the other readings…well, up in the air at this point, apart from this (which, if you’ve not read it, is excellent). Had thought about Herwig’s book on The Marne, which I’m finishing now, but the timing is all off. At any rate, you’ll hear more about this decision shortly.
5. And, finally, I think I’ll be able to sketch out some simple game-theoretic models for many of the topics we’ll consider, from the high politics of diplomacy, statecraft, and intrawar bargaining, to military strategy, to labor-management tensions at home, and to the dynamics of resistance and reprisals behind the front, etc., which should lend some unity to the whole thing. Let’s hope so, at least. Again, fingers crossed.

Broadly, I think that we can learn a lot from the war—sure, maybe not much about some things on which it’s an outlier—but specific instances of general trends can be awfully illuminating when we place them in theoretical context, and my hope is that the anniversary fever for the seminal tragedy in modern history can be put to good use (translation: my students are going to get ambushed with more science than they expect). Keep an eye on this space in the coming weeks and months as I try to figure out how to do just that.

 

A theory of neutrality rights in war – paper and slides

I’m giving a talk today at Maryland on a topic that’s pretty new to me—the laws of neutrality in war—though I guess I did hint about the genesis of this project several months ago. It’s a project that’s in its early stages, but it’s one I’m sufficiently excited about to publicize a bit, so here are links to a draft of the paper and the slides I’ll be using to confuse the audience today.

As I’m also hesitant to give said talk unshowered and in a *very* rumpled shirt, I’m cutting this short. Hopefully, though, there’ll be more to report in the days ahead.

Information problems and the end of the Russo-Japanese War

Turns out that teaching the Russo-Japanese War yesterday gave me a lot more food for thought—or, at a minimum, things I want to talk about—than I realized. Near the end of Connaughton’s account of the war, we see some contemporary puzzlement about why, despite destroying the Tsar’s fleet and driving the Russians from Manchuria, the terms of the Treaty of Portsmouth gave Japan no indemnity (just some interests on the Liaodong peninsula) and dictated a mutual withdrawal from Manchuria. This quote from the New York Times is telling (quoted on p. 344):

The judgment of all observers here…is that the [Russian] victory is as astonishing a thing as ever was seen in diplomatic history. A nation hopelessly beaten in every battle of the war, one army captured and the other overwhelmingly routed, with a navy swept from the seas, dictated her own terms to the victory.

But, really, is it all that puzzling? Just a few pages before, we learn some crucial facts about the military situation at war’s end: Japan totters near bankruptcy, while Russia, despite her dim record on the battlefield, has access to cheaper credit and the ability to continue to pour troops into the region. Both sides, moreover, seemed to know this. Japan couldn’t hold out too much longer in Manchuria itself, and Russian reinforcements likely could’ve taken advantage of the deteriorating Japanese position if the war were to continue (though, to be fair, the Revolution of 1905 was brewing at the time).

Still, it seems that by this time, Japan and Russia has similar expectations over what the rest of the war would look like, which according to informational accounts of war termination (see, inter alia, this, this, and this), can facilitate peaceful settlement, as states will strike a bargain that looks like the ultimate outcome (roughly) but saves the costs of getting all the way there. Granted, this doesn’t mean they’ll strike a bargain that reflects the current military situation—and the Treaty of Portsmouth was manifestly not that—but that reflects their shared assessment of what fighting to the finish would look like.

In the final accounting, did Russia pull off a diplomatic coup that produced a settlement at variance with what “should” have happened, given the course of the war? It depends on your perspective, I suppose, but if the “course of the war” is the story of the information transmitted to each side about (a) Russia’s ability to reinforce and (b) Japan’s ability to fund the war, then the answer would have to be a pretty emphatic “no.” It’s a subtle, but oft-missed point: accounts of war termination can explain why the final settlement might look nothing like the final battlefield dispositions yet still prove stable: a war fought to the finish might look quite a bit different than where the belligerents happen to be when they sue for peace.

(Incidentally, war termination is also the subject of today’s grad international security class…)

Colonel Blotto and France’s Defeat in World War II

Yesterday’s post on my favorite WWI books reminded me about another piece of diplomatic history I read in summer 2011: Ernest R. May’s Strange Victory. It’s a great account of just how, against everyone’s expectations—including the Wermacht generalship—Germany was able to conquer France in such a short time in 1940. There’s a frustratingly weak nod towards political science analysis at the end, largely based on personalities, but when the book is at its best, it’s (a) doing the hard work of figuring out exactly what happened (a contribution of history as a discipline that I think we tend to underestimate) and (b) essentially describing the equilibrium to a Colonel Blotto game.

Who’s this Colonel Blotto? Most game theorists will recognize the problem we represent with the good Colonel: he’s got to allocate limited defensive assets across a mountain and a pass, while his opponent has to choose between attacking either the mountain or the pass. (Let’s set aside, for now, the whole “why you might attack a mountain” question; this ain’t about geography.) The problem, of course, is that Colonel Blotto’s opponent would like to attack at the location the Colonel doesn’t defend, while he’d of course like to defend the point of attack. If the enemy knew the Colonel’s position, he’d attack elsewhere, and if the Colonel knew the enemy’s plans, he’d defend accordingly. The solution to such a game, with apologies to precisely how we might interpret mixed strategies, is to obscure your intentions—which the Nazis were, for the most part, able to do. The French, of course, fortified their eastern frontier with Germany, anticipating an attack along that axis (ha!), but the German plan, as we know, sent the materially and technologically inferior (at the time) Wermacht through BeNeLux and conquered France in a matter of weeks—all because they won the Blotto game.

It’s a long read, but—trust me—totally worth it.

Showing Restraint, Signaling Resolve: Slides

I’m headed to SUNY Buffalo this week for a min-conference on Mathematical Modeling of Political Behavior (thanks for the invite, Phil Arena), and to help tie my hands against spending all my time editing them, I’m putting the slides for my presentation, “Showing Restraint, Signaling Resolve,” up here on the blog.

I’ve presented this paper around quite a bit (see here and here)—and since it’s under review, I’m not going to put it up here—but the essential point is that coalition partners—specifically, the desire to ensure their cooperation—can have a profound impact on bargaining, signals, and the probability of war. Against strong targets, the desire to keep a skittish partner in the fold discourages a coalition leader from bluffing; so, although its partner “waters down” the threat, it helps discourage war. Against weak targets, preserving military cooperation discourages a coalition leader from signaling its resolve; instead, it acts like an irresolute state, tempting the coalition’s target to risk war. As it happens, this pattern shows up pretty strongly in the data (which, trust me, was no small relief), and while the empirics aren’t in the version currently under review, I’m sure they’ll show up somewhere eventually…

And it appears that Buffalo’s going to be a bit, ah, chilly:

 

 

 

 

 

 

 

 

 

 

 

Damn it.