World War I in Real Time: First Edition Problems

I’m teaching out of my World War I game theory textbook for the first time this semester, and as I worked through some early-morning class prep this morning, I noticed a tiny little error in Chapter 2. But worry not: all the equilibria still exist, and for the same reasons. It’s a typo, but one worth clarifying.

What’s the issue?

Section 2.2, “Commitment Problems and War,” motivates a game in which state A has to decide whether to launch a preventive war in light of the possibility that B, who’s rising in strength, might renege on the status quo in the future. And in describing A’s payoffs, I say that its best outcome of a peacefully honored status quo gives it 4, its worst outcome of passing on war only to see the status quo renegotiated is 1, and the middling outcome of launching a preventive war today is 2. That’s true whatever B’s strategy happens to be, because that strategy is preempted by A’s use of war.

That … makes sense.

But for some reason, in Figure 2.5 (rendered below), A gets 2 for the outcome of the (attack; honor) strategy profile and 3 for the (attack; renege) strategy profile. That’s…unnecessary. A should really get 2 for both, unless we want to say that attacking a B that would’ve honored the agreement is regrettable, but that’s not necessary for the story. It’s also not in my initial description of the payoffs.

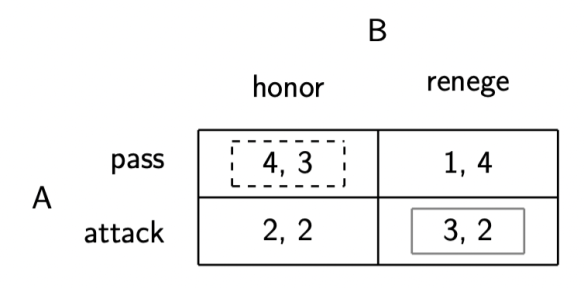
Now, as you’ll see, the Nash Equilibrium of the game (marked by the solid gray lines) is the same whether that offending 3 is in there or is replaced by the intended 2:

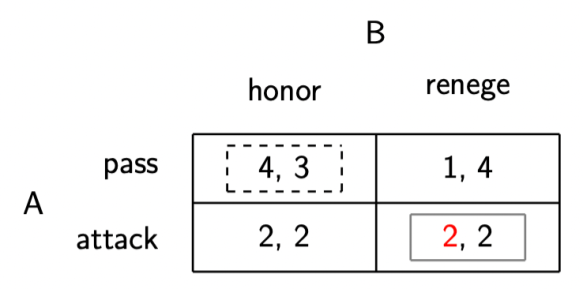
But I don’t want to let errors like this pass without some kind of note to adopters and students and whoever else has posts on this blog inflicted on them. So, apologies, dear reader(s). Let’s hope there aren’t too many more posts like this one forthcoming.

My own buffoonery aside, there’s a useful point here: forcing ourselves to “do the math” means we can more easily find, correct, and assess the consequences of mistakes in our premises and/or our reasoning. That’s always and everywhere a good thing for the social scientist.